ZéBuLoN, Numerical Microscope for Composites

copyright © ONERA 2008 - All rights reserved
Result of a finite elements numerical simulation (ZéBuLoN code) showing the field of plastic deformations in a micro-structure of a composite material with a metal matrix. The blue discs represent the long elastic fibers. It is the metal matrix that is subject to the deformations (green, yellow, red).

copyright © ONERA 2008 - Tous droits réservés
Analog calculation, with a finer mesh.

copyright © ONERA 2008 - All rights reserved
3D calculation of a composite micro-structure made up of elastic inclusions in an elasto-plastic metallic matrix [1].

The illustrations above are a representation of the micro-metric dimension of composite materials used, for example, in an aircraft engine. These materials, with remarkable thermo-mechanical properties, are made up of elastic components – long fibers or particle inclusions – set in a metal matrix. The images show the micro-structures of these materials calculated by a finite element method using the ZéBuLoN structures calculation code, developed by the  Ecole des Mines in Paris in partnership with Onera.

The mechanical simulations in these volumes at microscopic scale are used in the framework of multi-scale methods, developed at Onera by Jean-Louis Chaboche's team, and increasingly used in industry for designing the parts that are the most thermally and mechanically stressed.

The principle of the methods consists in alternating between the macro and micro scales. To calculate the stress field in a structure at macroscopic scale (see, for example, the disc in the figure below), we take a "macro" deformation. We then use specific transition rules to obtain the deformation at the microscopic scale. A simulation, like those the results of which can be seen above, gives the "micro" stresses, using the local behavior law. We then scale up the stress in the part using the laws of averaging.

To calculate the complete structure, we take the micro-structure into account by a "homogenizing" technique. The periodic homogenizing method used here owes a great deal to the French school of mechanics of the last forty years (FE2  method [2]).

Finally, the ZéBuLoN software, which can perform non linear calculations, is one of the rare finite elements codes that can support the case of large multi-scale simulations, notably due to its unique multi-domain parallelism capabilities.

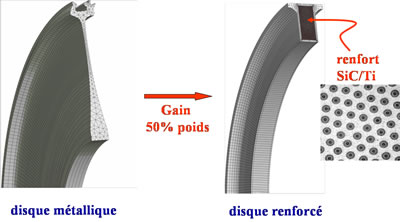
The inclusion of composites with metal matrices in a turbine disc (here an ANAM disc, Monoblock Blade Ring) reduces the mass to a spectacular degree. The non linear finite element calculations are a mandatory stage in the validation of the dimensioning and for the lifetime of these parts (EPICUR and EPICUR II programs).

Experimental set-up for traction-torsion tests on metal matrix composite tubes (Onera DMSM/CEMN laboratory). These tests contribute to establishing homogenizing rules and behavior laws and also to validating the structural resistance. There are only two other installations of this type in Europe with similar capacities.

Glossary

• [1] Elastoplastic
  Characterizes the behavior of a material with properties that are both plastic – irreversible deformations – and elastic – reversible deformations.
• [2] FE2 method
  One of the specific features of the approach taken at Onera lies in the direct integration of the change of scale process in each material point of the structure, a method known as FE2, or "Finite Elements squared". It is used to directly integrate the thermo-mechanical behavior of the micro-structure's phases into the non-linear analysis of the complete structure, without passing though the traditional intermediary of a law of macroscopic elasto-plastic behavior. 

The work of Pascale Kanouté and Serge Kruch, researchers in Onera's Metallic Materials and Structures Department.